Matematické modelovanie struny - model 1

(Mathematical Modelling of String - Model 1)

© Ing. Radovan Konečný - radkon, 2008

Pri vymýšľaní algoritmov pre výpočet zvuku sláčikového zboru metódou amplitúdových a frekvenčných modulácií ma napadla myšlienka naprogramovať model struny založený skôr na základných fyzikálnych princípoch správania sa struny.
Cieľom projektu je nájsť vhodný algoritmus, ktorým by bolo možné vytvárať zvuk virtuálneho hudobného nástroja na princípe modelovania. Algoritmus by bolo možné použiť:

• na výrobu samplov do syntezátora alebo ako „zvukový font“ (SoundFont) do lepších zvukových kariet PC,
• na vytvorenie programu pre PC - generátora zvuku v reálnom čase, na ktorom by sa dalo hrať cez pripojenú klávesnicu pripojenú cez rozhranie MIDI

Teoretický úvod

Ako som spomenul na začiatku, princíp modelovania vychádza zo základných fyzikálnych princípov. Tento model však nenapodobňuje správanie sa struny ako pružného natiahnutého telesa zloženého z množstva „kúskov“ struny, ale skôr napodobňuje výsledné správanie struny - stojaté vlny na strune spôsobené jej rozkmitaním. Kmitajúca struna vytvára celý rad znejúcich harmonických zložiek a pre každú harmonickú zložky som vytvoril samostatný model kmitajúceho hmotného telesa, ktorý je „naladený“ na požadovanú frekvenciu (1-násobok, 2-násobok, ... až N-násobok základnej frekvencie).
Pre kmitajúce teleso, napríklad zavesené na pružine, platí:

f = - k . x

kde f je sila pôsobiaca na teleso, k je konštanta pružiny reprezentujúca jej tuhosť a x je výchylka telesa z jeho rovnovážnej polohy. Tento vzťah určuje, že čím viac vychýlime teleso z jeho rovnovážnej polohy, tým väčšia sila pružiny pôsobí, aby sa teleso vrátilo do svojej rovnovážnej polohy.
Pre zrýchlenie takto zaveseného telesa platí:

a = f / m

kde a je zrýchlenie telesa a m je hmotnosť telesa (hmotnosť pružiny neuvažujeme).
Okamžitú rýchlosť v telesa určíme integrovaním zrýchlenia a okamžitú polohu x integrovaním rýchlosti v. Treba ešte poznamenať, že veličiny f, a, v a x sú v čase premenlivé.
Zjednodušený algoritmus, ktorý by toto realizoval, vyzerá nasledovne (syntax jazyka C alebo Java):

Takýto algoritmus spôsobí pri vychýlení telesa z rovnovážnej polohy jeho rozkmitanie a netlmené kmitanie. Reálne teleso by však bolo brzdené (napr. vzduchom), preto zavedieme do výpočtu tlmenie:

Hodnota konštanty tlmenie je blízka 1 (nesmie byť však > 1).

Kvôli zrýchleniu výpočtu ešte zmeníme delenie na násobenie (delenie je obvykle pre počítače oveľa pomalšou operáciou než násobenie) a na tento účel zmeníme význam konštanty hmotnost na konštantu nehmotnost, ktorá reprezentuje hodnotu 1/hmotnost:

Ešte si možno všimnúť, že v takejto forme algoritmu by sa dal výpočet ešte zjednodušiť a to vynechaním násobenia konštantou nehmotnost, pretože veľkosť sily f je určená konštantou tuhost a dve násobenia sú zbytočné a zvyšujú nároky na čas výpočtu:

Ako vidno z uvedeného kúsku programu, výpočet je až prekvapivo jednoduchý a ide vlastne o extrémne jednoduchý (a rýchly) algoritmus tlmeného (alebo aj netlmeného) oscilátora. Pre DSP (digital signal processor) by to bolo hračkou.

Jedno kmitajúce teleso by však nebolo až tak zaujímavé, pretože vytvára len harmonický signál (sínusový). Preto zavedieme takýchto telies N a vhodným nastavením ich hmotnosti a tuhosti (resp. konštanty tuhostKratNehmotnost) docielime, aby kmitali na násobkoch základnej frekvencie. (Pre zvýšenie frekvencie na 2-násobok treba zvýšiť tuhosť „pružiny“ na 4-násobok alebo znížiť hmotnosť 4-krát.)
Prirodzenou vlastnosťou struny je ešte to, že vyššie frekvenčné zložky tíchnu rýchlejšie a teda bolo treba nastaviť tlmenie jednotlivých kmitajúcich telies tak, aby táto požiadavka bola splnená. Čiže zložka so základnou frekvenciou znie najdlhšie.

Praktické výsledky

Po zrealizovaní N virtuálnych kmitavých telies sa ich pokojová poloha narúša aplikovaním veľmi krátkeho impulzu rýchlosti, čím sa teleso uvedie do pohybu. Ide o napodobnenie udretia kladivka do struny:

- udieranie kladivkom do virtuálnej struny

V uvedenej ukážke je energia daná z kladivka do kmitavého telesa rovnaká pre všetky telesá - pre všetky harmonické zložky.
Dobrou vlastnosťou takéhoto modelovania je, že energia udretia kladivka sa sčítava k energii už rozkmitaného telesa - dôsledkom je zvyšujúca sa amplitúda pri sérii úderov nasledujúcich krátko po sebe a pritom znie stále len jedna struna:

Časové priebehy veličín jedného kmitajúceho telesa tesne po údere kladivkom:

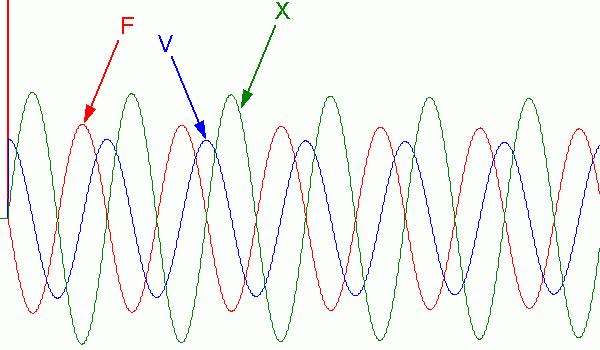
Mojim cieľom však bolo vytvoriť zvuk znejúci po dobu pôsobenia nejakého trvalého podnetu. Ako zdroj takéhoto podnetu som skúsil dať náhodný signál (biely šum) v domnienke, že to bude priblížením sa k pôsobeniu sláčika na strunu (akoby som v každom okamihu pôsobil na strunu náhodnou silou v náhodnom smere). Výsledkom je celkom zaujímavý zvuk - síce nie veľmi podobný husliam, ale jeho charakter ma milo prekvapil:

- virtuálna struna A4 pod pôsobením náhodného podnetu

- virtuálna struna A6 pod pôsobením náhodného podnetu

Vo zvukovej ukážke je počuť správanie sa virtuálnej struny aj po skončení pôsobenia podnetu.
Iná ukážka je z prípadu, kedy tlmenie kmitavých telies vyšších harmonických je rovnaké ako tlmenie telesa základnej frekvencie (v ukážke je počuť, že po skončení podnetu doznieva zvuk „ostrejšie“).

- virtuálna struna pod pôsobením náhodného podnetu pri rovnakom tlmení

Takýto prípad však nezodpovedá skutočným vlastnostiam struny. Avšak, vyššie harmonické sa rozoznejú lepšie a zvuk nie je toľko „šumový“.

Ďalšou otázkou bolo určenie frekvenčného spektra takto vyrobeného zvuku. Tu sa opäť dá experimentovať:

- spektrum 1 - zahraný akord 5 strún so spektrom podobným spektru pílovitého zvuku

- spektrum 2 - ten istý akord so spektrom oktáv a pár kvint - spektrum napríklad organu

Zvuk je síce zaujímavý, ale treba nájsť lepší spôsob rozoznenia struny, aby zvuk nebol toľko zašumený. Pri ťahaní sláčika po vibrujúcej strune táto struna kmitá aj v smere k/od sláčika a sláčik je v kontakte so strunou prevažne vtedy, keď smer pohybu sláčika a struny je rovnaký.